正規分布しているデータだと、分布から外れたデータを異常とできます。
要因となるデータ(特徴量)が複数ある場合はどうでしょう?
そんな時には、マハラノビス距離を算出して、異常かどうかを判断していきます。
本記事はこんな方におすすめです。

本記事の内容
- マハラノビス距離とは
- 実装方法
マハラノビス距離とは
特徴量が多変量で相関性がある場合に、その相関性も考慮した距離になります。
データの集まりから離れている方が、距離値が大きくなります。
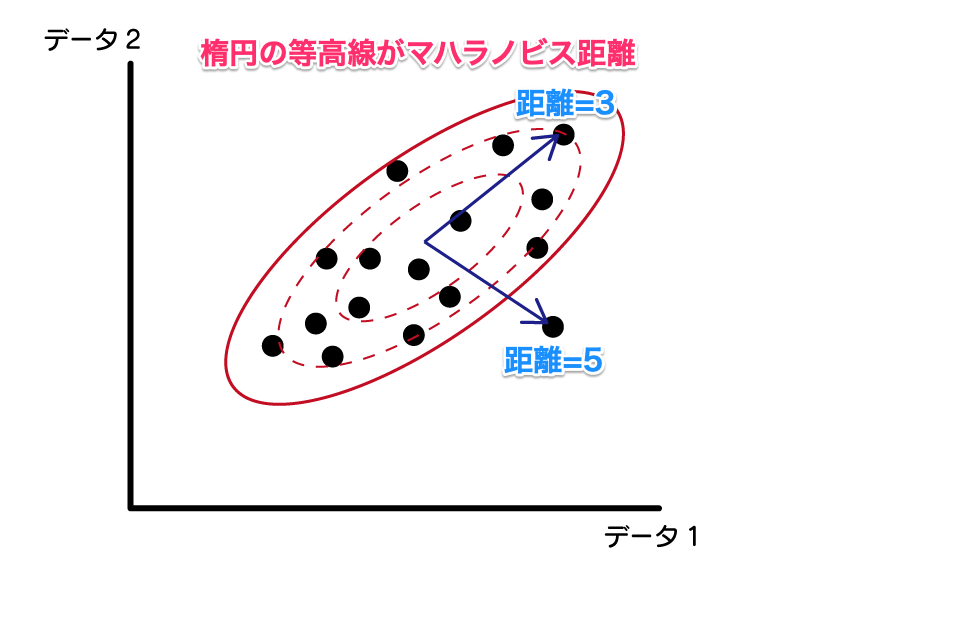
この距離がいいところは、1つ1つのデータでは異常とはわからないデータも異常として検知できる点です。
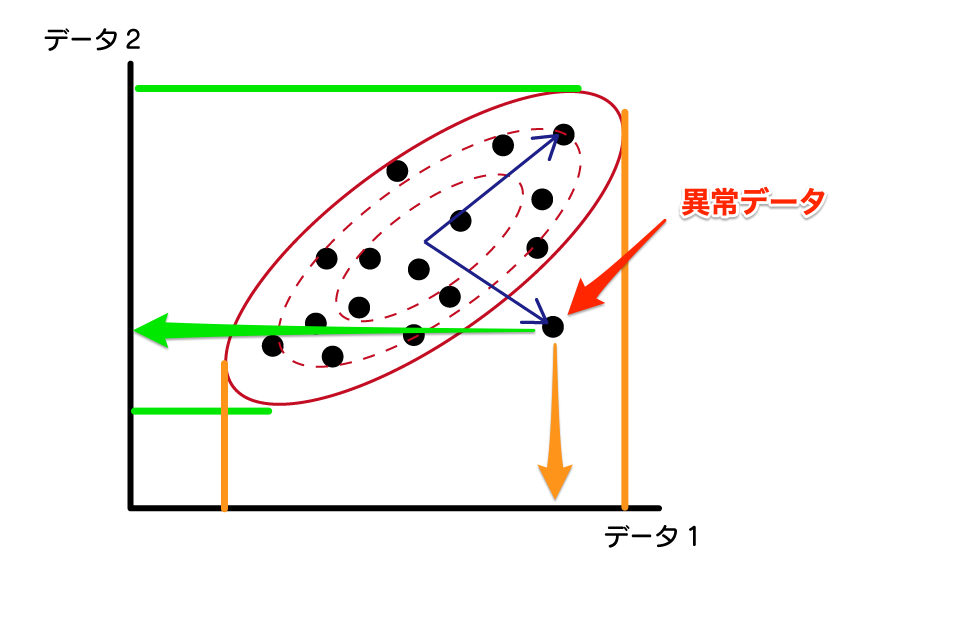
例えば、異常としたいデータは、データ1、2それぞれで見ると、他の正常なデータと同じ範囲に入っていることがわかります。
この場合、それぞれのデータで見ると異常とは判断できません。
マハラノビス距離は以下の式で表されます。
\( d = \sqrt{(x-\mu)^T\sum_{}^{-1}(x-\mu)} \)
\( x\): データ
\( \mu\): 平均
\( \sum_{}^{-1}\): 分散共分散行列
実装方法
さてでは、実装していきましょう。
データにはRに入っているDavisデータを使います。
データはコードと同じく、下記リンクにおいてあります。
計算には、関数化されたものと、numpyで計算したもを紹介します。
ライブラリ
以下のライブラリが必要になります。
必要なモノ
- pandas
- numpy
- scipy
- matplotlib
- seaborn
下の二つはデータをグラフで確認するためのものです。
ライブラリを読み込みましょう。
# CSV読み込み用
import pandas as pd
# 計算用
import numpy as np
from scipy.spatial import distance
# グラフ用
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set_style("whitegrid")
データの読み込み
CSVにしてある、Davisデータを読み込みます。
# Rに入っているDavisデータの読み込み
# https://www.kaggle.com/ravinduabey/davis-data-set
df = pd.read_csv("Davis.csv")
df.head()
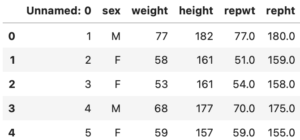
いくつかありますが、weightとheightのデータを使っていきます。
データの確認
weightとheightのデータをプロットしてみます。
# データをweightとheightに絞る df = df[['weight','height']] plt.scatter(df['weight'].values,df['height'].values)

異常なデータ2つほどありそうです。
共分散行列などの計算
先に、平均や共分散行列を計算します。
関数を使った計算で使います。
# 平均 mean = np.mean(data, axis=0) # 平均引いた値 data_m = data - mean # 共分散 cov = np.cov(data.T)
関数を使った方法
scipyのdistance.mahalanobisを使って計算していきます。
# distance.mahalanobisを使ってみた場合
result_1 = []
# データ: data[i], 平均値: mean, 共分散行列の逆行列: np.linalg.pinv(cov) から距離を計算
for i in range(len(data_m)):
result_1.append(distance.mahalanobis(data[i], mean, np.linalg.pinv(cov)))
結果をプロットしてみます。
# 結果 plt.plot(result_1)
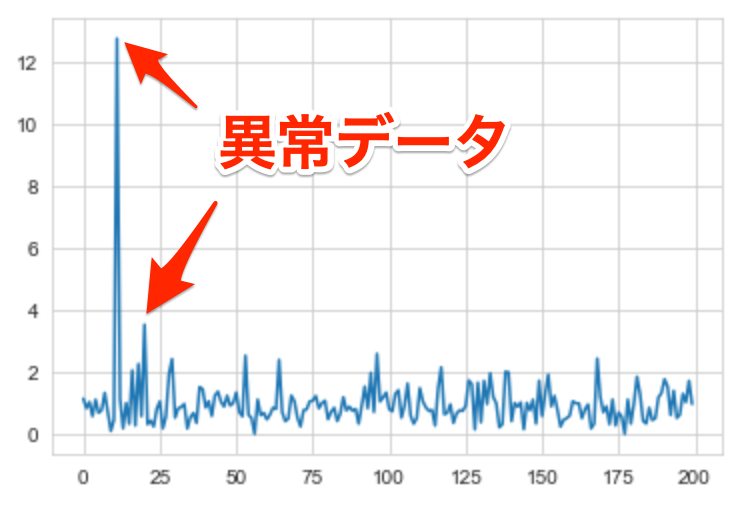
この値を使って異常かどうかを判断するのですが、どの数値を閾値にするかは決める必要があります。
今回の場合は、3 以上を異常とするのが良さそうです。
numpyで計算する方法
次は、numpyで計算します。
# pythonの関数の計算 result_2 = np.sqrt(np.sum(np.dot(data_m,np.linalg.pinv(cov))*data_m, axis=1))
といっても1行で済みます。
こちらの方がデータ量が多い時は計算が早いので、こちらを使った方が良いでしょう。
データも確認しましょう。
# 結果 plt.plot(result_2)
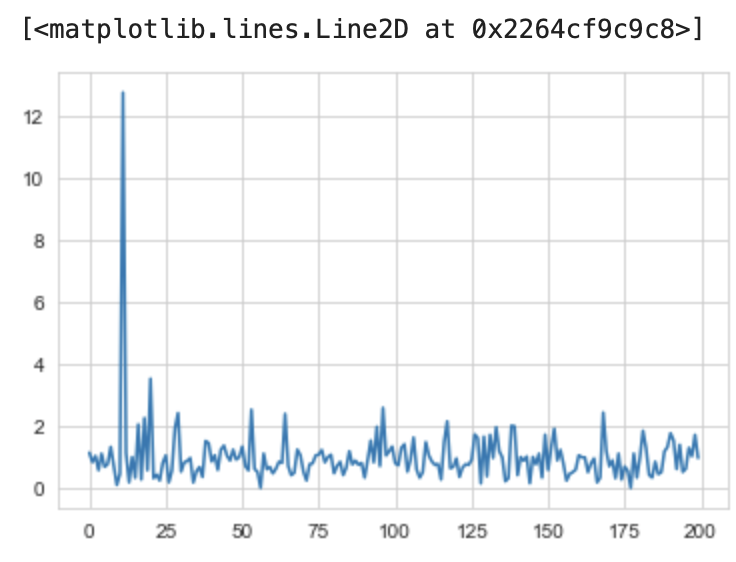
同じデータになりましたね。
今回はわかりやすいように、2変量のデータでしましたが、10変量とか多くなっても異常度として計算することができます。
今回のマハラノビスの計算は下記本にのっています。
